AN EQUATION is an algebraic statement in which the verb is "equals" = . An equation involves an unknown number, typically called x. Here is a simple example:
x + 64 = 100.
"Some number, plus 64, equals 100."
We say that an equation has two sides: the left side, x + 64, and the right side, 100.
In what we call a linear equation, x appears only to the first power, as in the equation above. A linear equation is also called an equation of thefirst degree.
The degree of any equation is the highest exponent that appears on the unknown number. An equation of the first degree is called linear because, as we will see much later, its graph is a straight line.
Now, the statement -- the equation -- will become true only when the unknown has a certain value, which we call the solution to the equation.
We can find the solution to that equation simply by subtracting:
| x | = | 100 − 64 |
| = | 36. | |
36 is the only value for which the statement "x + 64 = 100" will be true. We say that x = 36 satisfies the equation.
Algebra depends on how things look. As far as how things look, then, we will know that we have solved an equation when we have isolated x on the left.
Why the left? Because that's how we read, from left to right. "x equals . . ."
In the standard form of a linear equation -- ax + b = 0 -- x appears on the left, not the right.
In fact, we are about to see that for any equation that looks like this:
| x + a | = | b, |
| the solution will look like this: | ||
| x | = | b − a. |
Inverse operations
There are two pairs of inverse operations. Addition and subtraction, multiplication and division.
Formally, to solve an equation we must isolate the unknown(typically x) on the left.
ax − b + c = d.
To solve that equation, we must get a, b, c over to the right, so that xalone is on the left.
The question is:
Answer:
By writing it on the other side with the inverse operation.
100 − 64 = 36 implies 100 = 36 + 64;
and on the other, between multiplication and division:
| 10 2 | = | 5 | implies | 10 = 2· 5. |
Algebra is, after all, abstracted -- drawn from -- arithmetic.
And so, to solve this equation:
| ax − b + c | = | d |
| then since b is subtracted on the left, we will add it on the right: | ||
| ax + c | = | d + b. |
| Since c is added on the left, we will subtract it on the right: | ||
| ax | = | d + b − c. |
| And finally, since a multiplies on the left, we will divide it on the right: | ||
| x | = | d + b − c a |
We have solved the equation.
The four forms of equations
Solving any linear equation, then, will fall into four forms, corresponding to the four operations of arithmetic. The following are the basic rules for solving any linear equation. In each case, we will shift a to the other side.
1. If x + a = b, then x = b − a.
2. If x − a = b, then x = b + a.
| 3. If ax = b, then x = | b a | . |
| 4. If | x a | = b, then x = ab. |
In every case, we shifted a to the other side by means of the inverseoperation. Every linear equation can be solved by combining those fourformal rules.
When the operations are addition or subtraction (Forms 1 and 2 above), we call that transposing.
by changing its sign.
+ a goes to the other side as − a.
− a goes to the other side as + a.
Transposing is one of the most characteristic operations of algebra, and it is thought to be the meaning of the word algebra, which is of Arabic origin. (Arabic mathematicians learned algebra in India, from where they introduced it into Europe.) Transposing is the technique of those who actually use algebra in science and mathematics -- because it is skillful. And as we are about to see, it maintains the clear, logical sequence of statements. Moreover, it emphasizes that we do algebra with our eyes. When you see
| x + a | = | b, |
| then you immediately see that +a goes to the other side as −a: | ||
| x | = | b − a. |
The way that is often taught these days, is to add −ato both sides, draw a line, and add:

it disregards the logical sequence of statements and
therefore offers no preparation to read a calculus text,
for example.
What, after all, is the purpose of it? The purpose is to
transpose +a to the other side as −a. Therefore the
student should simply learn to transpose
A logical sequence of statements
In an algebraic sentence, the verb is typically the equal sign = .
ax − b + c = d.
That sentence -- that statement -- will logically imply other statements. Let us follow the logical sequence that leads to the final statement, which is the solution.
| (1) | ax − b + c | = | d | |
| implies | (2) | ax | = | d + b − c |
| implies | (3) | x | = | d + b − c . a |
The original equation (1) is "transformed" by first transposing theterms (Lesson 1). Statement (1) implies statement (2).
That statement is then transformed by dividing by a. Statement (2) implies statement (3), which is the solution.
Thus we solve an equation by transforming it -- changing its form -- statement by statement, line by line according to the rules of algebra, until x finally is isolated on the left. That is how books on mathematics are written (but unfortunately not books that teach algebra!). Each line is its own readable statement that follows from the line above -- with no crossings out
In other words, What is a calculation? It is a discrete transformation of symbols. In arithmetic we transform "19 + 5" into "24". In algebra we transform "x + a = b" into "x = b − a."
Problem 1. Write the logical sequence of statements that will solve this equation for x :
abcx − d + e − f = 0
To see the answer, pass your mouse from left to right
over the colored area.
To cover the answer again, click "Refresh" ("Reload").
Do the problem yourself first!
| (1) | abcx − d + e − f | = | 0 | |
| implies | (2) | abcx | = | d − e + f |
| implies | (3) | x | = | d − e + f . abc |
First, transpose the terms. Line (2).
It is not necessary to write the term 0 on the right.
Then divide by the coefficient of x.
Problem 2. Write the logical sequence of statements that will solve this equation for x :
| (1) | 2x + 5 | = | 27 | |
| implies | (2) | 2x | = | 27 − 5 = 22 |
| implies | (3) | x | = | 22 2 |
| implies | (4) | x | = | 11. |
Problem 3. Solve for x : (p − q)x + r = s
| x = | s − r p − q |
Problem 4. Solve for x : ab(c + d)x − e + f = 0
| x = | e − f ab(c + d) |
Problem 5. Solve for x : 2x + 1= 0
x = −½
That equation, incidentally, is in the standard form, namelyax + b = 0.
| Problem 6 . Solve: | ax + b | = | 0. | |
| x | = | − | b a | |
Each of these Problems illustrates doing algebra with your eyes. That is, the student should see the solution immediately. In the example above, the student should see that b will go to the other side as −b, and that a will divide.
That is skill in algebra.
Problem 7. Solve for x : ax = 0 (a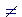 0).
0).
Now, when the product of two numbers is 0, then at least one of them must be 0 (Lesson 5). Therefore, any equation with that form has the solution,
x = 0.
We could solve that formally, of course, by dividing by a.
| x = | 0 a | = 0. |
| (Lesson 5.) | ||
Problem 8. Solve for x :
| 4x − 2 | = | −2 |
| 4x | = | −2 + 2 = 0 |
| x | = | 0. |
Problem 9. Write the sequence of statements that will solve this equation:
| (1) | 6 − x | = | 9 |
| (2) | −x | = | 9 − 6 |
| (3) | −x | = | 3 |
| (4) | x | = | −3. |
When we go from line (1) to line (2), −x remains on the left. For, the terms in line (1) are 6 and −x.
We have "solved" the equation when we have isolated x -- not −x -- on the left. Therefore we go from line (3) to line (4) by changing the signs on both sides. (Lesson 6.)
Alternatively, we could have eliminated −x on the left by changing all the signs immediately:
| (1) | 6 − x | = | 9 |
| (2) | −6 + x | = | −9 |
| (3) | x | = | −9 + 6 = −3 |
| Problem 10. Solve for x : 3 − x | = | −5 | |
| x | = | 8 | |
Problem 11. Solve for x :
| 5 − 2x | = | −11 |
| −2x | = | −11 − 5 |
| 2x | = | 16 Lesson 6 |
| x | = | 8 |
Problem 12. Solve for x:
| 3x − 15 2x + 1 | = 0 |
(Hint: Compare Lesson 5, Problem 18.)
x = 5.
Transposing versus exchanging sides
| Example 1. | a + b = c − x |
We can easily solve this -- in one line -- simply by transposing x to the left, and what is on the left, to the right:
x = c −a − b.
| Example 2. | a + b = c + x |
In this Example, +x is on the right. Since we want +x on the left, we can achieve that by exchanging sides:
c + x = a + b
Note: When we exchange sides, no signs change.
The solution easily follows:
c + x = a + b − c
In summary, when −x is on the right, it is skillful simply to transpose it. But when +x is on the right, we may exchange the sides.
Problem 13. Solve for x :
| p + q | = | r − x − s | |
| Transpose: | |||
| x | = | r − s − p − q | |
Problem 14. Solve for x :
| p − q + r | = | s + x | |
| Exchange sides: | |||
| s + x | = | p − q + r | |
| x | = | p − q + r − s | |
Problem 15. Solve for x :
| 0 | = | px + q | |
| px + q | = | 0 | |
| px | = | − | q |
| x | = | − | q p |
Problem 16. Solve for x :
| −2 | = | −5x + 1 |
| 5x | = | 1 + 2 = 3 |
| x | = | 3 5 |
Canceling
x + b + d = c + d.
d appears on both sides. Therefore, we may cancel them.
x + b = c.
Theoretically, we can say that we subtracted d from both sides.
Finally, on solving for x:
x = c − b.
Problem 17. Solve for x :
x² + x − 5 = x² − 3
Cancel the x²'s:
| x − 5 | = | −3 |
| x | = | −3 + 5 = 2. |
Problem 18. Solve for x :
x − a + b = a + b + c
Cancel the b's but not the a's. On the left is −a, but on the right is +a. They are not equal.
Transpose −a:
| x | = | a + a + c |
| x | = | 2a + c. |
The unknown on both sides
Example 3. Solve for x :
| 4x − 3 | = | 2x − 11. |
| 1. Transpose the x's to the left and the numbers to the right: | ||
| 4x − 2x | = | −11 + 3. |
| 2. Collect like terms, and solve: | ||
| 2x | = | −8 |
| x | = | −4. |
This is another example of doing algebra with your eyes. You shouldsee that 2x goes to the left as −2x, and that −3 goes to the right as +3.
As a general rule for solving any linear equation, we can now state the following:
Problem 19. Solve for x :
| 15 + x | = | 7 + 5x |
| x − 5x | = | 7 − 15 |
| −4x | = | −8 |
| x | = | 2. |
Problem 20. Solve for x :
| 1.25x − 6 | = | x | ||
| 1.25x −x | = | 6 | ||
| (1.25 − 1)x | = | 6 | On combining the like terms on the left. | |
| .25 x | = | 6 | ||
| x | = | 24. | On multiplying both sides by 4. | |
Problem 21. Remove parentheses, add like terms, and solve for x :
| (8x − 2) + (3 − 5x) | = | (2x − 1) − (x − 3) |
| 8x − 2 + 3 − 5x | = | 2x − 1 − x + 3 |
| 3x + 1 | = | x + 2 |
| 3x − x | = | 2 − 1 |
| 2x | = | 1 |
| x | = | 1 2 |
Simple fractional equations
| Example 4. | x 2 | = 4. |
Since 2 divides on the left, it will multiply on the right:
| x | = | 2· 4 |
| = | 8. | |
Problem 22. Solve for x :
| −x 5 | = | 3 |
| −x | = | 15 |
| x | = | −15. |
| Problem 23. | x 4 | = | 1 2 | |||
| x | = | 4· | 1 2 | = 2. | ||
Example 5. Solve for x:
| 4 x | = 5. |
Solution. In the standard form of a simple fractional equation, x is in the numerator. But we can easiy make that standard form by taking thereciprocal of both sides.
| x 4 | = | 1 5 | ||
| This implies | ||||
| x | = | 4 · | 1 5 | |
| = | 4 5 | . |
| Problem 24. | 2 x | = | 1 3 | |
| x 2 | = | 3 | ||
| x | = | 6. | ||
Example 6. Fractional coefficient.
| 3x 4 | = | y |
| Since 4 divides on the left, it will multiply on the right: | ||
| 3x | = | 4y. |
| And since 3 multiplies on the left, it will divide on the right: | ||
| x | = | 4y 3 |
| In other words, | 3 4 | goes to the other side as its reciprocal, | 4 3 | . |
| Note that | 3 4 | is the coefficient of x : |
| 3x 4 | = | 3 4 | x | . |
Coefficients go to the other side as their reciprocals!
| Problem 25. | 2x 3 | = | a | |
| x | = | 3a 2 | ||
| Problem 26. | 5 8 | x | = | a − b | ||
| x | = | 8 5 | (a − b) | |||
| Problem 27. | 4 5 | x + | 6 | = | 14 | ||
| 4 5 | x | = | 14 − 6 = 8 | ||||
| x | = | 5 4 | · 8 = 10. | ||||
| Problem 28. | A | = | ½xB | |
| Exchange sides: | ||||
| ½xB | = | A | ||
| x | = | 2A B | ||
The reciprocal of ½ is 2.
Problem 29. The Celsius temperature C is related to the Fahrenheit temperature F by this formula,
| F | = | 9 5 | C + 32 |
| F | = | 9 5 | · 10 + 32 |
| = | 18 + 32 | ||
| = | 50° | ||
b) Solve the formula for C.
| 9 5 | C + | 32 | = | F | |
| 9 5 | C | = | F − 32 | ||
| C | = | 5 9 | (F − 32) | ||
c) What is the Celsius temperature when the Fahrenheit temperature
c) is 68°?
| C | = | 5 9 | (68 − 32) |
| = | 5 9 | · 36 | |
| = | 5· 4 | ||
| = | 20° | ||






0 comments:
Post a Comment